
머신러닝의 지도학습은 크게 분류와 회귀로 나뉜다.
간단하게 정리하면 예측하려는 타깃값이
범주형 데이터라면 '분류'문제, 수치형 데이터면 '회귀'문제다.
분류(Classification)
: 어떤 대상을 범주에 구분해 넣는 작업

머신러닝에서 분류는 피처에 따라 어떤 대상을 유한한 범주(타깃값)으로 구분하는 방법이다.
여기서 중요한 점은 타깃값, 즉 예측하려는 값이 범주형 데이터라는 것이다.
분류 문제는 크게 이진분류와 다중분류로 나뉜다.
- 이진분류: 타깃값이 두 개
- 다중분류: 타깃값이 세 개 이상
범주형 데이터
범주형 데이터는 객관식 문제와 같이 선택지가 있는 값이다.
개와 고양이를 구분하는 문제, 스팸 메일과 일반 메일을 구분하는 문제, 검사 결과가 양성인지 음성인지 구분하는 문제 등
유한한 선택지 중 하나로 구분이 가능할 수 있는 문제 모두 분류에 속한다.
숫자로도 표현이 가능하다. 성별을 남자를 1, 여자를 0으로 표현하거나, 수치형 자료를 1~10과 같은 범위로 나타낸다면 이 또한 범주형 데이터로 볼 수 있다.
회귀(Regression)
: 독립변수와 종속변수 간 관계를 모델링하는 방법. 임의의 연속적인 어떤 숫자를 예측
회귀가 분류와 다른 점은 종속변수(타깃값)이 범주형 데이터가 아니라는 것이다.
회귀 문제에서는 타깃값이 수치형 데이터다.
예를 들면, 내년도 경제 성장률을 예측하거나 배달이 도착할 시간을 예측하는 문제 등이 있다.
이처럼 회귀는 정해진 클래스 없이 임의의 수치를 출력한다.
- 선형회귀(Linear Regression)
선형회귀는 널리 사용되는 대표적인 회귀 알고리즘이다.
선형이란 말에서 짐작할 수 있듯이 특성이 하나인 경우 어떤 직선을 학습하는 알고리즘이다.
즉, 선형회귀는 특성을 가장 잘 나타낼 수 있는 직선을 찾는 것이다.
<단순선형회귀>
학습시간이 시험 성적에 미치는 영향을 예로 살펴 보겠다.
| 독립변수 | 종속변수 |
| 학습시간 | 시험성적 |
시험 성적은 0점, 10점, 50점 등 연속된 숫자 값으로 나타낼 수 있다.
먼저, 선형회귀는 간단하게 표현하면
Y = aX + b
처럼 1차 함수로 표현할 수 있다.
여기에서 x를 학습시간, y를 시험성적으로 바꾸면 다음과 같다.
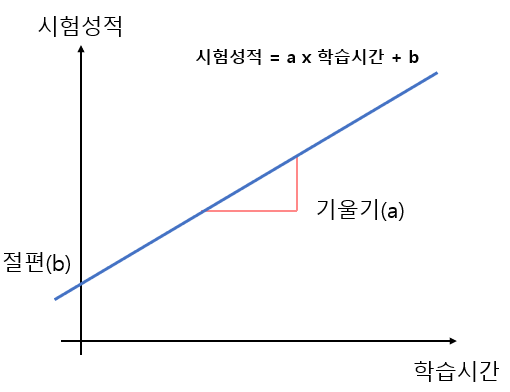
이와 같이 독립변수 하나와 종속변수 하나의 사이의 관계를 나타낸 모델링 기법을
단순 선형회귀라고 한다.
선형회귀는 특성을 잘 나타낼 수 있는 직선 찾는 것이다. 이 직선을 그리기 위해서는 무엇이 필요할까?
=> 기울기(a)와 절편(b)을 찾는 것이다.
여기서 회귀계수는 a, 기울기가 된다.
회귀계수
회귀계수는 독립변수가 종속변수에 미치는 영향력의 크기를 알려주는 지표다.
이를 통해 독립변수가 종속변수에 얼마나 영향을 주었는지 알 수 있게 한다.
<다중 선형 회귀>
독립변수 여러 개와 종속변수 한 개 사이의 관계를 나타낸 모델링 기법을 다중 선형 회귀라고 한다.
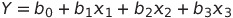
b1 ~ b3이 회귀계수다.
분류와 회귀 평가지표
- 분류 평가지표
분류 평가지표로 여러 가지가 있다. 그중 가장 기본적인 지표인
오차 행렬, 로그 손실, ROC 곡선, AUC에 대해 알아보겠다.
1. 오차행렬(confusion matrix)
오차행렬은 실제 타깃값과 예측한 타깃값이 어떻게 매칭되는지 보여주는 표다.
혼동행렬이라고 하기도 한다.
다음과 같이 네 가지 경우를 표 형태로 나타낸다.
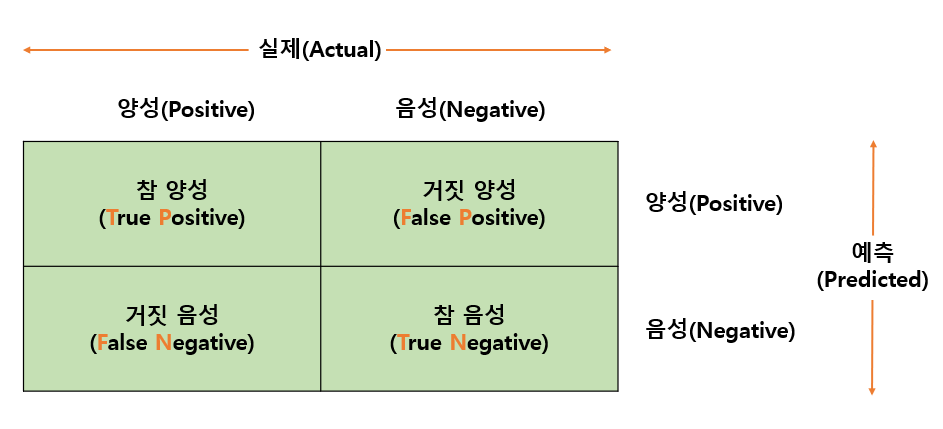
- 참 양성(TP): 실제 타깃값이 양성 예측도 양성
- 거짓 양성(FP): 실제 타깃값이 양성인데 예측은 음성
- 거짓 음성(FN): 실제 타깃값이 음성인데 예측은 양성
- 참 음성(TN): 실제 타깃값이 음성 예측도 음성
* 검출하기 원하는 상태를 보통 양성으로 지정한다.
오차행렬을 활용한 주요 평가지표로는
정확도, 정밀도, 재현율, F1 점수가 있다. 이 지표들 모두 값이 클수록 좋은 지표다.
- 정확도 (accuracy)
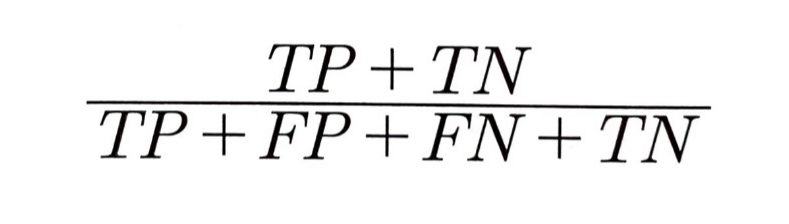
- 실젯값과 예측값이 얼마나 일치되는지 비율로 나타낸 평가지표
- 전체 값 중 참 양성(TP)과 참 음성(TN)이 차지하는 비율
- 예측 결과와 실제값이 동일한 수 / 전체 데이터 수
- 정확도를 사용하는 경우는 많지 않다
- 정밀도 (precision)
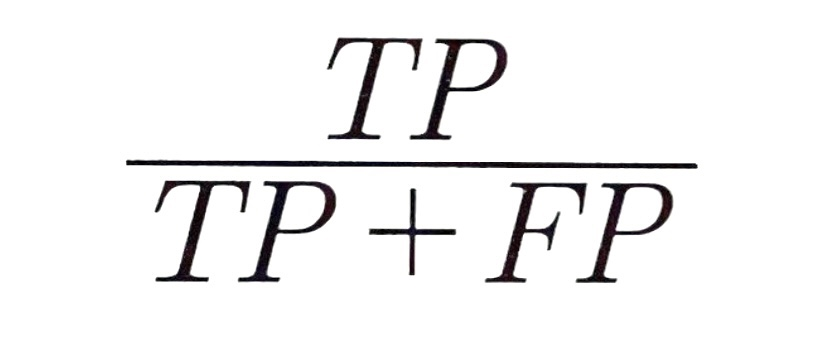
- 양성 예측의 정확도
- 양성이라고 예측한 값(TP + FP) 중 실제 양성인 값(TP)의 비율
- 음성을 양성으로 잘못 판단하면 문제가 발생하는 경우 사용
음성을 양성으로 잘못 판단하면 문제가 발생하는 경우는 어떤 게 있을까?
스팸 메일 필터링을 예로 들 수 있다.
스팸메일 -> 양성, 일반 메일 -> 음성이라고 하자.
이 문제에서 양성을 음성으로 잘못 판단했다면 스팸을 일반 메일로 잘못 판단하여 받은 메일함에 스팸 메일이 하나 들어올 것이다. 이 경우 스팸 메일을 삭제한다면 그만이다.
하지만 반대로 음성을 양성으로 잘못 판단하게 된다면 일반 메일을 스팸으로 잘못 판단하게 되어 중요한 메일인데 받지 못하는 경우가 있을 수 있다.
이 경우처럼 음성을 양성으로 잘못 판단했을 때 더 문제가 될 때 정밀도를 사용할 수 있다.
- 재현율 (recall)
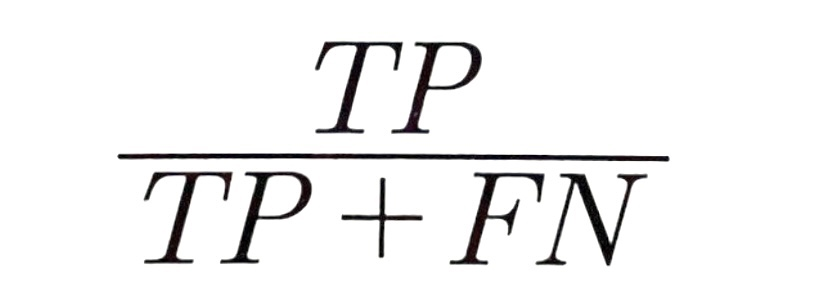
- 실제 양성 값(TP + FN) 중 양성으로 잘 예측한 값(TP)의 비율
- 민감도(sensitivity) 또는 참 양성 비율(TPR: True Positive Rate)라고 한다
- 양성을 음성으로 잘못 판단하면 문제가 되는 경우 사용
양성을 음성으로 잘못 판단하면 문제가 발생하는 경우는
암을 진단하는 상황을 예로 들 수 있다.
양성인데 음성이라고 잘못 판단한다면 암인데 암이 아니라고 진단하게 되는 것이므로 큰 문제가 발생한다.
반대라면, 오진이지만 생명에 큰 문제가 되지 않는다.
- F1 점수 (F1 score)
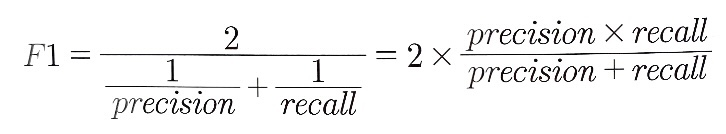
- 정밀도와 재현율을 조합한 평가지표
- 정밀도와 재현율 둘 중 어느 하나에 편중하지 않고 적절히 조합하고 싶을 때 사용
- 정밀도와 재현율의 조화 평균으로 구한다
2. 로그 손실(log loss)
- 분류 문제에서 타깃값을 확률로 예측할 때 기본적으로 사용하는 평가지표
- 값이 작을수록 좋은 지표
3. ROC 곡선과 AUC
- ROC(Receiver Operating Characteristic) 곡선
- 참 양성 비율(TPR)에 대한 거짓 양성 비율(FPR) 곡선
- 참 양성 비율(TPR): 양성을 얼마나 잘 예측하는지 나타내는 지표 (재현율과 같은 개념) 특이도라고도 한다.
- 거짓 양성 비율(FPR): 실제 음성인 데이터를 양성으로 잘못 예측한 비율
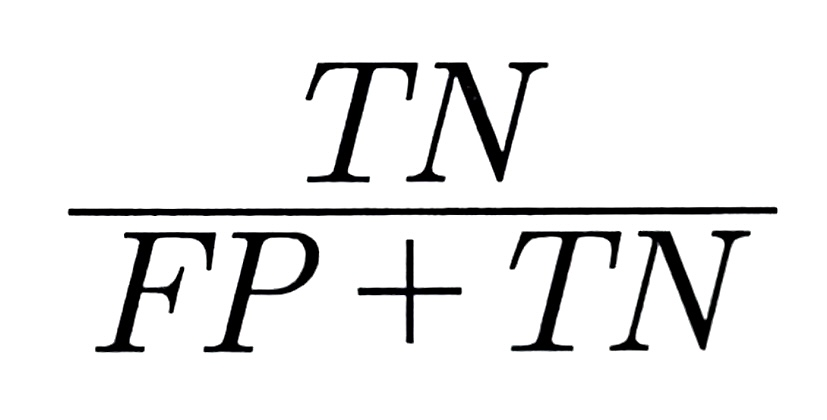
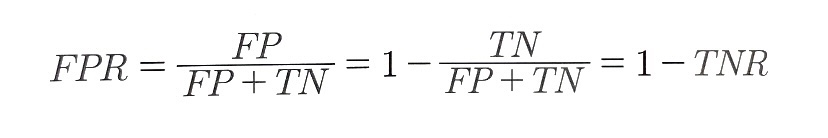
- AUC(Area Under the Curve)
- ROC 곡선 아래 면적
- 기본적으로 예측값이 확률인 분류 문제에서 사용
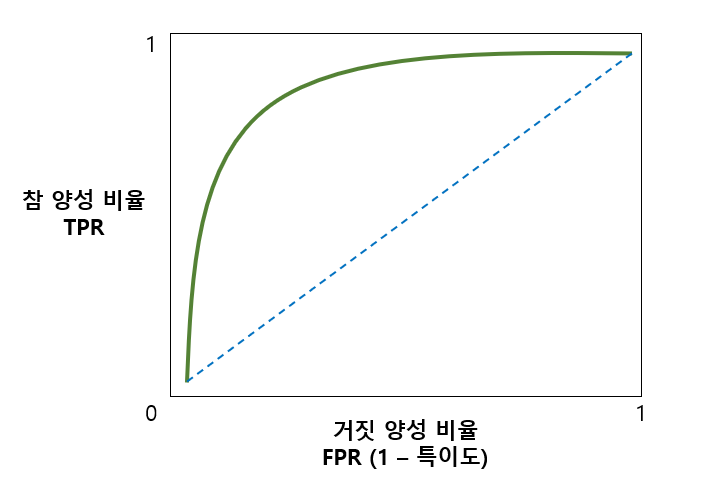
가운데 점선은 완전 무작위로 분류시 ROC 곡선이다. (예측 값이 없는 분류기)
무작위로 분류했으므로 가장 성능이 나쁘다고 할 수 있다.
즉, ROC 곡선은 무작위로 분류한 가운데 점선과 가까울수록 모델 성능이 떨어지고
위쪽으로 멀어질수록 성능이 좋은 모델이다.
FPR, TPR 모두 비율이므로 0부터 1사이의 값을 갖는다.
AUC는 곡선 아래 면적을 의미하기 때문에 100% 완벽하게 분류한다면 AUC는 1이고,
완전 무작위로 분류하면 0.5가 된다.
-> 모델 성능이 좋을 수록 AUC가 크다!
| 타깃값(이산값)으로 예측 시 분류 평가지표: 정확도, 정밀도, 재현율, F1점수 타깃 확률로 예측 시 분류 평가지표: 로그손실, AUC |
- 회귀 평가지표
회귀 모델을 훈련해 최적의 회귀계수를 구할수 있다. 최적 회귀 계수를 구하려면 예측값과 실젯값의 차이,
즉 오차를 최소화해야 한다.
오차가 작다는 것은 주어진 데이터에 회귀 모델이 잘 들어맞다는 뜻이다.
회귀 모델의 성능을 측정하는 평가지표는 다음과 같다.
*회귀 평가지표 값이 작을수록 모델 성능이 좋다.
MAE

- 평균 절대 오차(Mean Absolute Error)
- 실제 타깃값과 예측 타깃값 차의 절댓값 평균
MSE
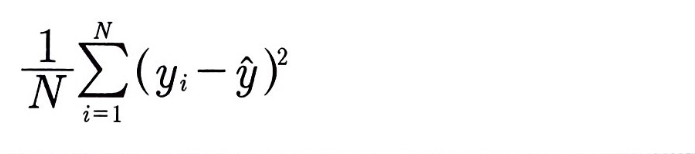
- 평균 제곱 오차(Mean Squared Error)
- 실제 타깃값과 예측 타깃값 차의 제곱의 평균
RMSE
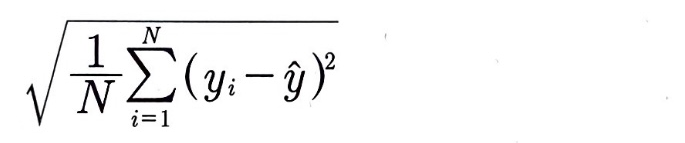
- 평균 제곱근 오차(Root Mean Squared Error)
- MSE에 제곱근을 취한 값
- 작을 수록 좋은 모델
MSLE
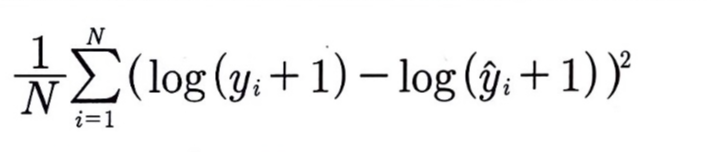
- Mean Squared Log Error
- MSE에서 타깃값에 로그를 취한 값
RMSLE
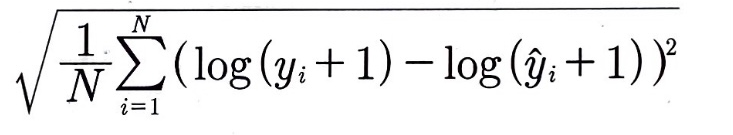
- Root Mean Squared Log Error
- MSLE에 제곱근을 취한 값
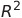

- 결정계수. 예측 타깃값의 분산 / 실제 타깃값의 분산
- 다른 지표와 다르게 1에 가까울수록 모델 성능이 좋다
사이킷런의 metrics 라이브러리를 활용해 회귀 평가지표 값을 구할 수 있다.
import numpy as np
# MAE, MSE, MSLE, R2 임포트
from sklearn.metrics import mean_absolute_error, mean_squared_error, mean_squared_log_error, r2_score
true = np.array([1, 2, 3, 2, 3, 5, 4, 6, 5, 6, 7, 8, 8]) # 실제값
preds = np.array([1, 1, 2, 2, 3, 4, 4, 5, 5, 7, 7, 6, 8]) # 예측값
MAE = mean_absolute_error(true, preds)
MSE = mean_squared_error(true, preds)
RMSE = np.sqrt(MSE)
MSLE = mean_squared_log_error(true, preds)
RMSLE = np.sqrt(mean_squared_log_error(true, preds))
R2 = r2_score(true, preds)
# 출력
print(f'MAE:\t {MAE:.4f}')
print(f'MSE:\t {MSE:.4f}')
print(f'RMSE:\t {RMSE:.4f}')
print(f'MSLE:\t {MSLE:.4f}')
print(f'RMSLE:\t {RMSLE:.4f}')
print(f'R2:\t {R2:.4f}')

실제값과 예측값을 임의로 정하고, 사이킷런의 metrics 라이브러리를 활용해
각 평가지표에 따라 값을 쉽게 구할 수 있다.
상관계수
두 변수 사이의 상관관계 정도를 수치로 나타낸 값을 상관계수라고 한다.
보통 약자 r로 표기한다.
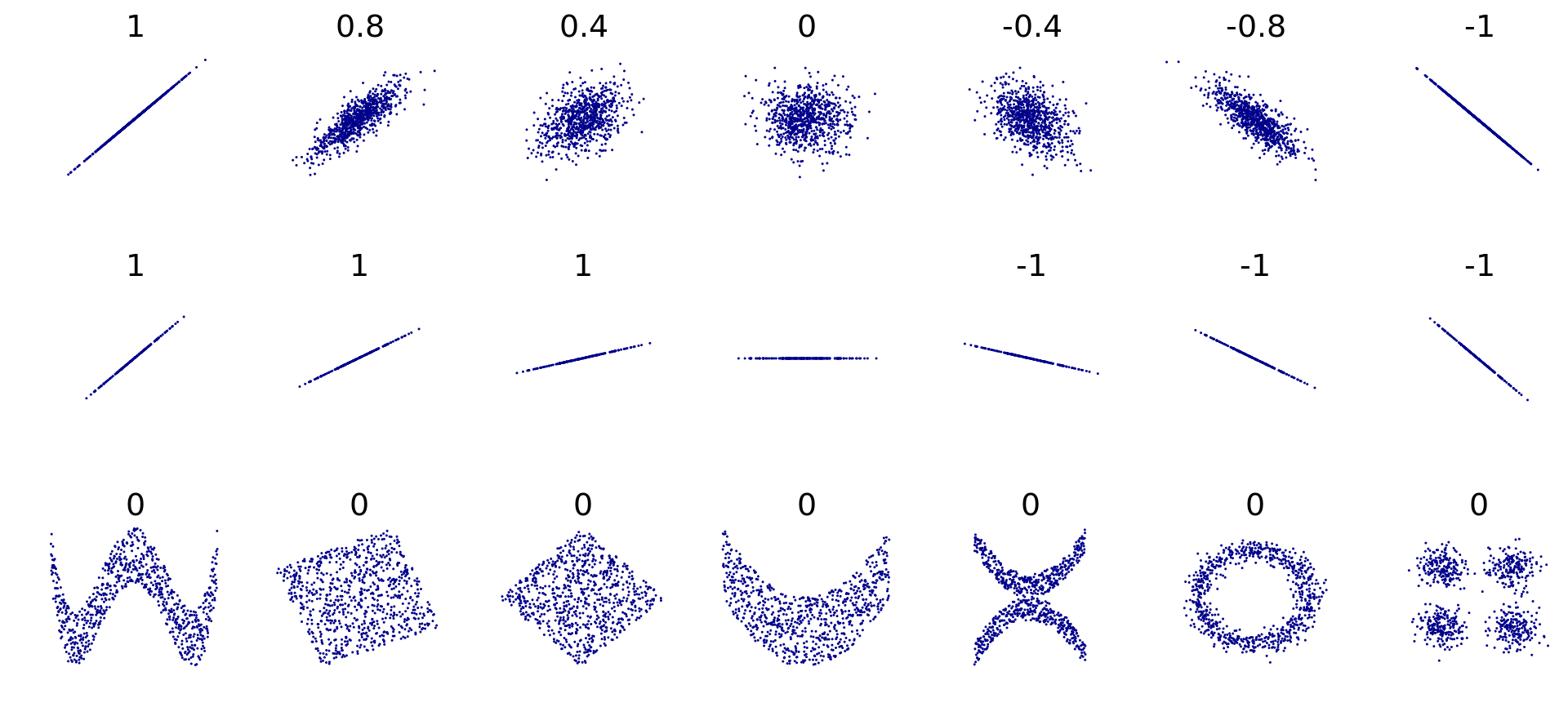
여러 상관계수 중 가장 많이 쓰는 선형 회귀 상관계수는 피어슨 상관계수다.
- 선형 상관관계의 강도와 방향을 나타낸다
- -1부터 1 사이의 값을 갖는다
- 상관계수가 음수면 음의 상관관계, 양수면 양의 상관관계가 있다고 한다
- 1 또는 -1에 가까울수록 상관성이 큰 것이고, 0에 가까울수록 상관성이 작다
참고 교재

머신러닝·딥러닝 문제해결 전략 | 신백균
[머신러닝·딥러닝 문제해결 전략 - chapter5]
'ML,DL' 카테고리의 다른 글
| [머신러닝/딥러닝] 향후 판매량 예측 경진대회: 분석정리 및 시각화 (0) | 2022.11.19 |
|---|---|
| [머신러닝/딥러닝] 안전 운전자 예측 경진대회: 분석정리 및 시각화 (0) | 2022.11.07 |
| [머신러닝/딥러닝] 범주형 데이터 이진분류 경진대회: 분석정리 및 시각화 (1) | 2022.10.04 |
| [머신러닝/딥러닝] 피처 스케일링: min-max 정규화, 표준화 (2) | 2022.09.19 |
| [머신러닝/딥러닝] 데이터 인코딩(레이블, 원-핫) (1) | 2022.09.19 |



